import numpy as np
import matplotlib.pyplot as plt
- 확률적 경사하강법
- 단점: 학습률(lr)을 학습하는 동안에 변경할 수 없다.
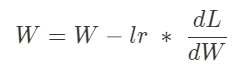
→ W : 파라미터(가중치, 편향) lr : 학습률(learning rate) dL/dW : 변화율
class Sgd_ function:: init
→ 학습률 learning_rate를 초기 입력받는다.
class Sgd:
""" SGD: Stochastic Gradient Descent
W = W - lr * dL/dW
"""
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rateclass Sgd_ function:: update
파라미터 params와 변화율 gradients가 주어지면 파라미터들을 갱신하는 메소드
params, gradients: 딕셔너리. {key: value, ...}
def update(self, params, gradients):
for key in params:
# W = W - lr * dl/dW
params[key] -= self.learning_rate * gradients[key]
필요한 function
def fn(x, y):
"""f(x, y) = (1/20) * x**2 + y**2"""
return x**2 / 20 + y**2
def fn_derivative(x, y): # 함수 fn의 미분값
return x/10, 2*yTest
# Sgd 클래스의 객체(인스턴스)를 생성
sgd = Sgd(0.95)
# ex01 모듈에서 작성한 fn(x, y) 함수의 최솟값을 임의의 점에서 시작해서 찾아감.
init_position = (-7, 2)
# 신경망에서 찾고자 하는 파라미터의 초깃값
params = dict()
params['x'], params['y'] = init_position[0], init_position[1]
# 각 파라미터에 대한 변화율(gradient)
gradients = dict()
gradients['x'], gradients['y'] = 0, 0
# 각 파라미터들(x, y)을 갱신할 때마다 갱신된 값을 저장할 리스트
x_history = []
y_history = []
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
gradients['x'], gradients['y'] = fn_derivative(params['x'], params['y']) # gradients 갱신
sgd.update(params, gradients)
for x, y in zip(x_history, y_history):
print(f'({x}, {y})')Result
(-7, 2)
(-6.335, -1.7999999999999998)
(-5.733175, 1.6199999999999997)
...
(-0.4727262060886904, -0.11629947400607987)
(-0.42781721651026483, 0.10466952660547188)
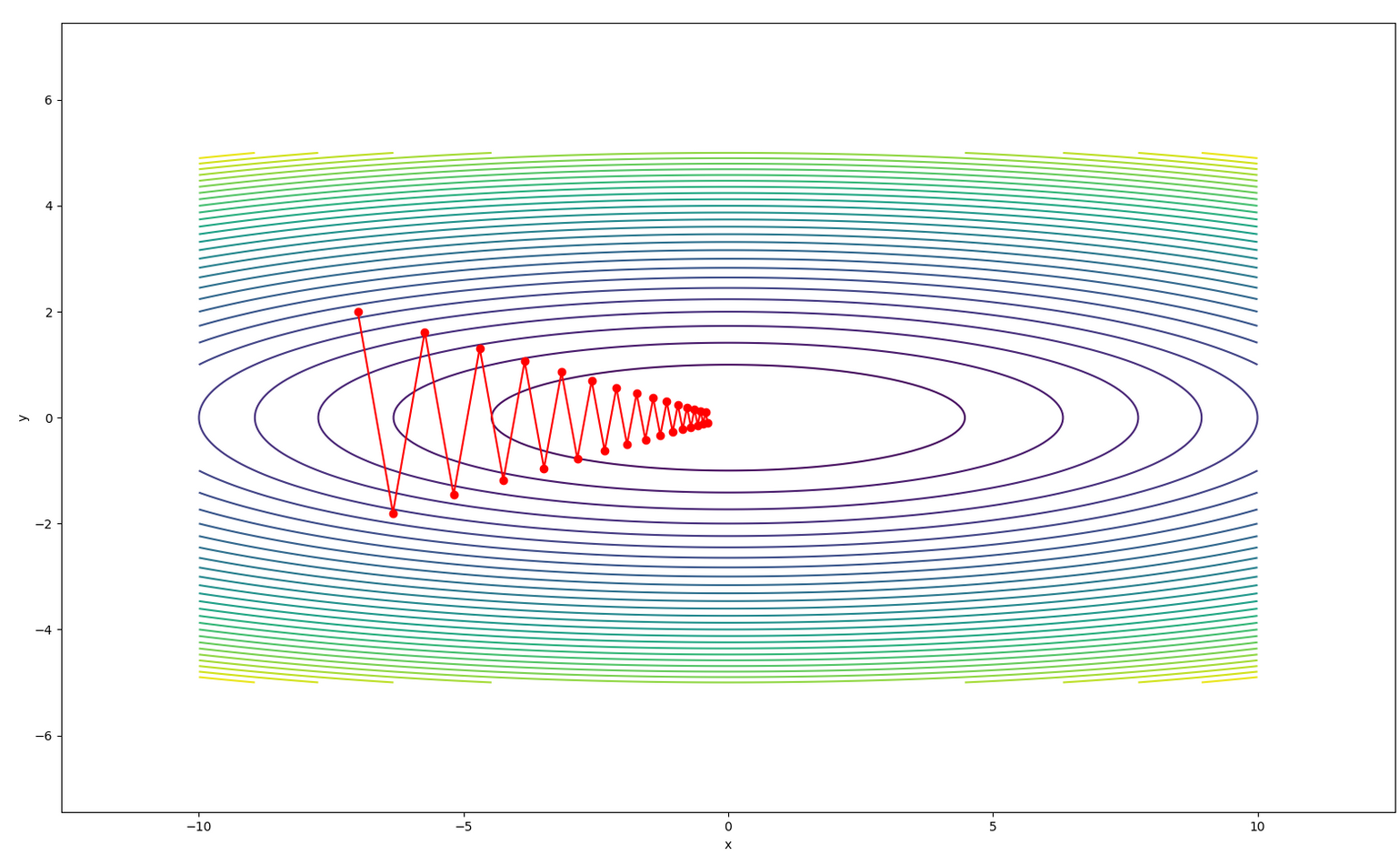
(-0.3871745809417897, -0.09420257394492468)f(x, y) 함수를 등고선으로 표현
x = np.linspace(-10, 10, 200)
y = np.linspace(-5, 5, 200)
X, Y = np.meshgrid(x, y)
Z = fn(X, Y)
plt.contour(X, Y, Z, 30)
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
# 등고선 그래프에 파라미터(x, y)들이 갱신되는 과정을 추가.
plt.plot(x_history, y_history, 'o-', color='red')
plt.show()
- 최종 코드
import numpy as np
import matplotlib.pyplot as plt
class Sgd:
""" SGD: Stochastic Gradient Descent
W = W - lr * dL/dW
"""
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
def update(self, params, gradients):
for key in params:
# W = W - lr * dl/dW
params[key] -= self.learning_rate * gradients[key]
def fn(x, y):
"""f(x, y) = (1/20) * x**2 + y**2"""
return x**2 / 20 + y**2
def fn_derivative(x, y): # 함수 fn의 미분값
return x/10, 2*y
if __name__ == '__main__':
# Sgd 클래스의 객체(인스턴스)를 생성
sgd = Sgd(0.95)
# ex01 모듈에서 작성한 fn(x, y) 함수의 최솟값을 임의의 점에서 시작해서 찾아감.
init_position = (-7, 2)
# 신경망에서 찾고자 하는 파라미터의 초깃값
params = dict()
params['x'], params['y'] = init_position[0], init_position[1]
# 각 파라미터에 대한 변화율(gradient)
gradients = dict()
gradients['x'], gradients['y'] = 0, 0
# 각 파라미터들(x, y)을 갱신할 때마다 갱신된 값을 저장할 리스트
x_history = []
y_history = []
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
gradients['x'], gradients['y'] = fn_derivative(params['x'], params['y']) # gradients 갱신
sgd.update(params, gradients)
for x, y in zip(x_history, y_history):
print(f'({x}, {y})')
x = np.linspace(-10, 10, 200)
y = np.linspace(-5, 5, 200)
X, Y = np.meshgrid(x, y)
Z = fn(X, Y)
plt.contour(X, Y, Z, 30)
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
# 등고선 그래프에 파라미터(x, y)들이 갱신되는 과정을 추가.
plt.plot(x_history, y_history, 'o-', color='red')
plt.show()'Python > Python 딥러닝' 카테고리의 다른 글
| Keras를 이용한 mnist 숫자 데이터 분류(1) (0) | 2020.07.13 |
|---|---|
| Keras에서 개발 과정, 활성화함수, 옵티마이저, 손실함수, 평가지표란? (0) | 2020.07.13 |
| [tensorflow]텐서 선언하기, 즉시 실행모드를 통한 연산, @tf.function (0) | 2020.07.10 |
| Tensorflow의 기본 개념 : Tensor, Rank, Flow, Graph, Node, Edge, Session (0) | 2020.07.10 |
| 유용한 Datasets를 얻을수 있는 사이트들 (0) | 2020.07.10 |
